프롤로그
이 글은 천개의 고원 “1790년 – 강렬하게-되기, 동물-되기, 지각 불가능하게-되기” 중 음악-되기라는 내용을 살펴보는 것입니다. 이를 통하여 ‘되기’라는 개념을 이해하고 그 중 음악의 특수한 환경에서의 되기 개념을 이해하려는 이해-되기를 위함입니다. 대상 글에서 나온 내용 중 저자들인 들뢰즈와 가타리가 들었던 실재 음악가들의 예를 찾아보면서 음악-되기를 보다 현실감있게 이해하기 위함입니다. 자, 그럼 음악이 되어 볼까요?
음악–되기 이해를 위한 ‘되기’ 이해
프랑스 원문에는 ‘되기’가 ‘devenir’, 영어로는 ‘become(becoming)’으로 표기되어 우리말 그대로 ‘되기’가 됩니다. 프랑스 원문에는 ‘생성’이라는 뜻이라고도 합니다. 그러므로 되기는 ‘생성’ 이라고도 할 수 있지요. 여성-되기는 여성-생성, 아이-되기는 아이-생성, 동물-되기는 동물-생성이 될 수 있겠지요. 그러니까 되기는 앞의 단어를 만나 앞의 단어가 ‘되는’ 생성을 말하는 것 같습니다. 여기서 생성이란 단어는 당연히 중요한 주제일 것입니다. 생성은 단지 앞 단어의 물리적인 모양이나 모방의 형태가 되는 것이 아니라 실제 될 수 없으나 되려고 하는 분자적인 합성과 이미지의 방출을 통한 생성을 나타냅니다. 예를 들어 누군가 개-되기를 하고자 한다면 개의 짖음과 같은 성대모사나 모방은 중요하지 않고 (또한 술을 많이 먹는 것과도 관계없고) 개와 관련된 이미지와 그 이미지의 방출을 노력 하는 것이라 합니다. 아무튼 되기는 모방이 아닌 무언가 대상의 이미지를 만들어 내는 분자적인 노력, 생성과정이라 할 수 있겠습니다.
그럼 음악-되기는 음악을 모방하는 것이 아닌 음악과 관련된 이미지나 빠름과 느림의 속도 등을 나타내는 생성인건가요? 그럼 음악의 이미지나 속도 등은 무엇일까요? 아니 음악이란 무엇일까요? 음악이라는 구체적인 대상을 끄집어낼수록 더 어려워지는 것 같습니다. 하지만 복잡해지는 김에 조금 원론적으로 돌아가 점과 선에 관련한 이야기로부터 시작하여 음악이 무엇이고 음악의 횡단선에 대한 이야기를 해보도록 하겠습니다.
저자들은 인간이라는 중심점, 남성과 어른이라는 지배적인 점 그리고 아이, 여성과 같은 지배적이지 않은 점을 상정하며 선과 점에 관하여 이야기를 시작합니다. 이때 선이 점에 종속되는 것을 나무형 (리좀과 대비되는 체계에 의한) 이라고 부릅니다. 이때 생성 (되기)의 선은 점들 사이를 지나가고 점들 중간을 통해 돌출됩니다. 즉, 둘 사이 경계선, 도주선이라 합니다. 그 도주선은 하나의 블록을 형성하며 두 점과는 아무것도 아닌 땅을 형성합니다.
점은 곧 과거의 기억, 회상이며 아이-되기에 있어 유년기의 회상 (모방) 만으로는 아이-되기는커녕 이와 대립되는 것으로 취급됩니다.
선 ⇽ ⇾ 점
블록 ⇽ ⇾ 회상
생성 ⇽ ⇾ 기억
이라는 대척점을 가지는 것이지요. 기억은 점 체계입니다.
시간의 관계에서 나타내자면,
옛 지금 현재 = 시간 흐름 (수평선), 운동
옛 지금 표상 = 시간 질서 (수직선), 지층

점 체계와 선 체계
점 체계의 특성은
- 수평, 수직의 기본선 – 좌표기능
- 수평선은 수직으로 중첩, 수직선은 수평으로 이동
- 점과 점을 연결하는 연결선 및 사선 가능
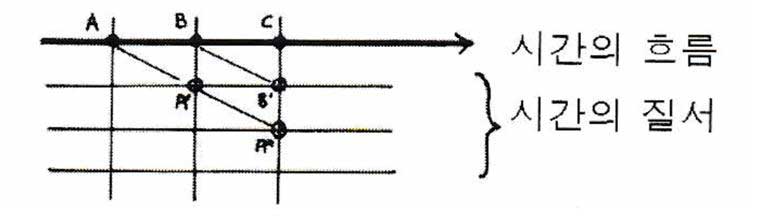
점 체계는 나무형이며 그램분자적이고 영토화, 재영토화와 관계되며 점체계에서 선들은 연결선의 역할만 할뿐 점에 종속됩니다. 한편, 선 체계는 다선적 체계에 따라 선, 사선을 해방시킵니다. 여기에서는 점은 선에 종속되는 것이죠. 그리고 점의 체계는 예술가들에게는 도약 (도주)의 발판입니다. 이를 위해서는 조작이 허용되어야 하는데 그를 위해서는 수직, 수평선에 달라붙는 것이 아닌 지각할 수 없는 사선을 만들어야 합니다.
음악의 재현
위의 점과 선체계를 음악에 접목해보면 다음과 같습니다.
수평, 수직의 기본선은 수평의 선율 (시간의 흐름)과 수직의 화음으로 구분됩니다. 즉, 선율과 화음을 수평과 수직으로 나눌 수 있습니다.
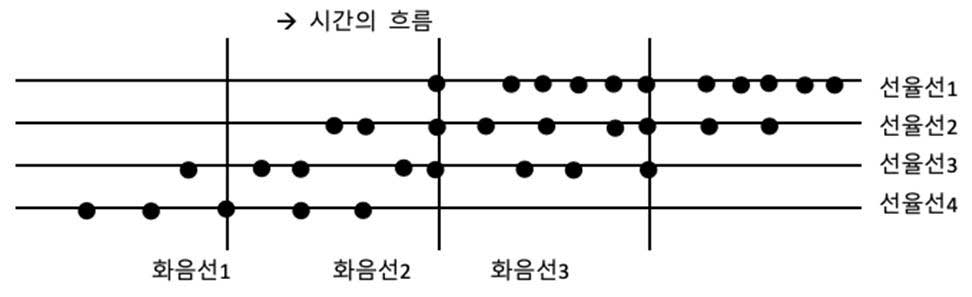
이것을 실재 악보로 예를 들면,

위의 실제 악보에서 보듯이 시간의 흐름에 따라 수평의 각 선율선들 (여기에선 5개의 선율선, 다성 선율이 있습니다) 이 이동하고 음표라는 점들을 따라 수직적으로 화음들이 쌓아지고 있습니다. ‘지각할 수 없는 사선’을 만들기 위해서는 위의 악보와 같이 여러개의 선율 체계가 만들어 져야 할 겁니다. 즉, 다성 음악이 되어야 합니다. 그래야만 단선율에서 불가능한 사선을 만들어 낼 수 있기 때문입니다. 비록 다소 극단적인 예이겠지만, 실재 악보에서 볼 수 있듯이 중심 선율은 첫마디에서 선율선1을 따라 이동하다 두 번째 끝부분에서 선율선 2를 따라 사선으로 이동하며 다시 선율선 1 이동하는 횡단선 (사선)을 볼 수 있습니다. 그래서 실재 각 선율선을 따로 들을 때와는 달리 다성의 선율이 결합되었을 때 비로소 사선을 타고 이루어지는 가상의 음과 리듬의 블록이 형성되는 것입니다.
다성음악이 무엇인지에 대한 간단한 예를 영상으로 보시죠.
프랑스 작곡가 및 음악이론가인 피에르 불레즈 (Pierre Boulez, 1925 ~ 2016)는 횡단선 위 음의 블록이 움직이며 이때 수평/수직의 좌표가 없다고 합니다. 그 이유는 점 연결이 아니고 박동이 없는 시간 (위에 언급한 가상의 블록) 이기 때문입니다. 즉, 점, 좌표, 박자가 없는 상태. 리듬 블록을 형성합니다. 빠름과 느림이 있는. 사선은 복잡한 음의 선이고 음의 공조 것이죠. 이제 다선적 체계에서는 점은 선이 되고 수직/수평선은 사선이 되며 사선은 횡단선이 됩니다.
“나는 기억을 증오한다. 회상을 증오한다.”
음악가들은 가끔 이렇게 이야기합니다. 얼마 전에 만난 음악가로부터 이와 똑같은 이야기를 들었습니다. 그는 요즘 그 동안 들었던 음악을 전혀 듣지 않고 있다고 합니다. 왜냐하면 자신의 기억속의 틀에 박힌 음악에 너무 종속되어 이것이 음악을 만드는데 방해가 되고 있다는 것이지요. 그것은 아마 기억의 점 체계를 파괴하려는, 창조의 선 체계를 생성하려는 몸부림이 아닐까 싶습니다.
저자들은 사선, 블록-선의 전형을 빈 악파에서 찾은 듯합니다. 빈 악파는 과거 빈에서 활동한 음악가들을 말하는데 대표적으로 하이든, 모차르트, 베토벤을 말합니다. 그들은 고전주의시대를 마감하고 개인이 음악 안에 있는 낭만주의 음악의 시작을 연 작곡가들로 평가 받습니다. 그들은 점, 수직, 수평선의 새로운 체계를 찾아냈으며 그 이후 또 다른 창조행위가 다른 음악가들을 통하여 이루어졌습니다. 즉, 점 밖에서 불안정한 사선을 긋고 창조된 선위에서 블록을 떠다니게 하면서 말입니다. 이런 생성행위들로 인하여 분자적이고 반음계적인 현대 클래식 음악에까지 이르게 한 것입니다.
음악되기
그렇다면 음악의 내용은 무엇일까요? 저자들은 여성-되기, 아이-되기, 동물-되기, 분자-되기라고 하는데요. 아마도 중심적이고 지배적인 점인 인간과 남성, 어른의 점들을 탈주하는 열린 의미로서의 여성, 아이, 동물, 분자가 되는 것이라 생각되는데요. 더 구체적인 것은 아이-되기의 예들을 보면서 느껴보도록 하겠습니다.
슈만은 소년시절을 생각하면서 1838년 어린이의 정경이라는 표제를 붙여 출판하였는데요. 이 작품들이 탄생은 그의 연인이었던 클라라와의 편지에서 시작되었다 합니다. 그 편지들 중 클라라가 ‘ 가끔 당신은 어린이같이 생각됩니다’ 라는 말을 듣고 만든 곡들이라 합니다. 슈만은 이 곡을 연주할 때면 사람들에게 대단한 인상을 주고 자신이게도 그렇다라고 하였습니다. 이는 단지 어린 시절을 회상한 곡이라기보다는 자신의 기억과 회상을 이미지화하여 현재의 내가 음악을 통하여 아이가 되었다라는 것이겠지요. 그 결과 오늘날까지 아이의 순수함을 잘 표현한 명곡이라고 칭송 받는 것 같습니다.
이렇듯 실재 아이의 리토르넬로는 음악이 아니지만 음악의 아이 되기는 ‘아이’ 라는 생성의 블록을 형성합니다. 리토르넬로는 음악의 고유한 내용의 블록이라고 합니다. 여기서 리토르넬로란 전통적인 의미에서 리토르넬로는 서양 클래식 음악에서 나오는 간주곡이라고 하는데요. 지속적으로 주제 사이사이에 나오는 반복되는 구절을 말합니다. 하지만 저자들이 말하고 있는 리토르넬로는 보다 영역을 확대하는 것 같은데, 음악에서 반복되고 강조되는 주제를 말하는 것 같습니다. 그리고 저자들은 리토르넬로의 반복 속에서 차이의 변주곡을 통한 탈주를 노립니다.
위의 곡은 모차르트의 곡인데요. 너무나 익숙하고 유명한 곡이죠. 이렇게 익숙한 곡도 다양한 변주를 통하여 멋진 곡으로 다시 생성됩니다. 이 작품 안에서는 12개의 변주를 통하여 테마의 각 음표가 이중화되고, 테마자체가 내부에서 이중화됩니다. 이를 통하여 리토르넬로를 사선/횡단선에 의해 처리하고 고정되어 있는 영토성에서 떼어냅니다. 그러므로 음악은 리토르넬로를 탈영토화 함으로써 이루어지는 능동적이고 창조적 조작이라고 할 수 있습니다. 앞에서 말했듯이 점의 체계를 바탕으로 하는 조작이라는 것이죠.
여기서 탈영토화는 이중적인 의미를 담고 있는데요. 아이-되기의 탈영토화를 통하여 음악가 자신도 아이가 되고 아이 자신도 아이가 된다는 것입니다. 또한 음악, 동물-되기에서도 인간은 인간의 범위를 넘는 동물의 ‘이것’이 되고 동물은 밤, 죽음, 기쁨 등이 됩니다. 이렇듯 ‘되기’는 언제나 둘을 통해 진행, 생성할 대상, 생성하는 자가 탈영토화의 탈주선을 타고 다른 영토를 생성합니다.
저자들은 목소리의 예를 드는데, 목소리의 탈영토화가 그것입니다. 목소리가 악기화 되었을 때 분자-되기가 된다는 건데요. 분자적인 것은 원소적인 것, 우주적인 것, 이것은 소통 가능한 것이 됩니다. 이런 소통가능 능력은 형식을 해체하고 다양한 위도, 경도를 가지며 다양한 느림과 빠름으로 형식을 넘어 변주 확장이 가능해 집니다. 앞의 예 에서 본 모차르트의 변주가 가능하다는 겁니다.
프랑스 작곡가 올리비에 메시앙 (Olivier Messiaen, 1908 ~ 1992) 은 원소적인 것, 우주적인 것이 블록, 우주의 섬유, 사선 또는 복합 공간을 만든다 하였습니다. 또한 음악은 인간의 특권은 아니며 우주도 코스모스도 모두 리토르넬로를 만들고 있다고 합니다. 음악에서는 인간만이 아닌 동물, 원소, 사막 등 ‘자연’을 가로지르는 탈영토화의 역량이 중요하며, 오히려 인간에게서 음악적이지 않은 것, 자연에서 이미 음악적인 것이 문제가 됩니다.
인간의 비음악적인 음이
음의 음악-되기와 더불어
블록을 만들어야 한다
에필로그
저자들은 여기에서 이야기의 끝을 맺습니다. 하지만 제 생각에는 우리의 실재 생활에 중요한 것은 이 문구 다음의 이야기일 거라 생각 합니다. 짧지만 조금 더 이야기를 진행하고 글을 맺으려 합니다.
인간의 비음악적인 음
음악-되기는 나 자신이 음악이 되기를 생각하게 합니다. 저자들은 음악 안에서 작곡가들이 동물이 되기도 하고 아이가 되기도 하고 여성이 되기도 하며 드디어 분자가 되어 우주와 소통하지만, 이것은 지극히 공급자 (작곡가) 적인 것으로 제 개인적인 음악-되기는 나 자신이 음악이 되는 것입니다. ‘내’가 음악이 되고 ‘음악’이 내기 되는. 비록 모두가 작곡가일수 없는 노릇이기에 우리들은 작은 것에서 시작할 수도 있을 것입니다.
리듬–되기
걸을 때 리듬이 되어 보기.
음–되기
말할 때 음을 만들어 보기.
화음–되기
함께 무엇인가를 해보기. 자유로운 결합을 통하여 편안함과 긴장감을 느껴 보기.
음악–되기
우리의 환경을 음악으로 상상해보기. 그리고 그 환경에서 나는 어떤 악기일지 상상해보기.
음의 음악–되기
그리고 그 되기가 상상되는 음악을 찾아보기.
우리는 모두 분자가 되어 자유로이 이 공간을 우주를 날아다닐 수 있을 겁니다. 우리는 땅 위에서만이 아닌 그곳에서 만날 수 있을 겁니다.
이제 그 시작인 리듬을 걸음걸음에 담아 보세요. 아마 스윙 리듬이 어울릴 수도 있을 겁니다.



