“지도제작으로서의 도표 개념이 원인과 결과, 문제제기와 대답, 입구와 출구의 불일치를 전제로 한다고 얘기하면, 사람들은 “원래 그랬던 거 아니었어?”라고 되묻습니다. 그리고 당연하다는 듯 입구와 출구의 일치로 향하곤 합니다.”1
이 문장을 읽으면서 피식 웃음이 났다. “원래 그랬던 거 아니었어?”라고 이미 알고 있었던 것처럼 말하지만 실제로는 피상적으로 알 뿐 그 본질에 이르지 못하는 경우가 얼마나 많은가. 지도 그리기란 무엇인가. 그것은 본질적인 것과 본질적이지 않은 것을 구분하고 오직 본질적인 것만을 전경으로 줌 인(zoom in) 하는 행위라고 할 수 있다. 수학에는 그런 예들이 많다. 그 중에 하나가 「쾨니히스베르크 다리 건너기 문제」이다.
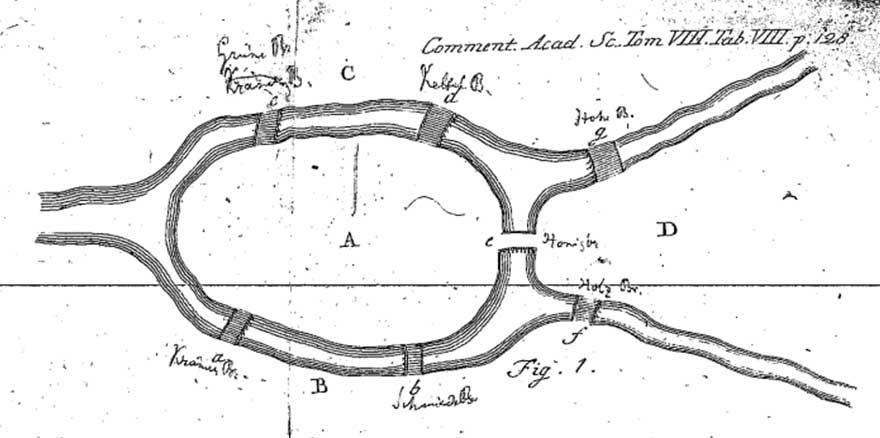
프로이센 왕국의 쾨니히스베르크시2를 흐르는 프레겔 강에는 크나이프호프(A)와 롬세(D)라는 두 개의 하중도(河中島)가 있다. 이 독특한 지형의 강을 건너기 위해 일곱 개의 다리가 건설되었는데, 바로 여기서 시작된 문제다. 문제는 다음과 같다.
“쾨니히스베르크시의 한 가운데는 프레겔 강이 흐르고 있고 여기에는 가운데 섬들과 연결되어 있는 일곱 개의 다리가 있다. 그 다리들을 한 번씩만 차례로 모두 건널 수 있겠는가?”
오일러(Leonhard Euler)는 이 문제를 [그림 2]와 같이 네 개의 정점(Vertex; A~D)과 각 정점을 연결하는 일곱 개의 간선(Edge; a~g)으로 도식화해 1735년에 논문을 발표했다. 이때 모든 간선을 한 번씩 방문하는 유한 그래프(Finite Graph)를 일컬어 오일러 경로(Eulerian Path)라 하는데, 오일러는 쾨니히스베르크의 다리 건너기 문제가 오일러 경로가 아님을 증명한 것이다.
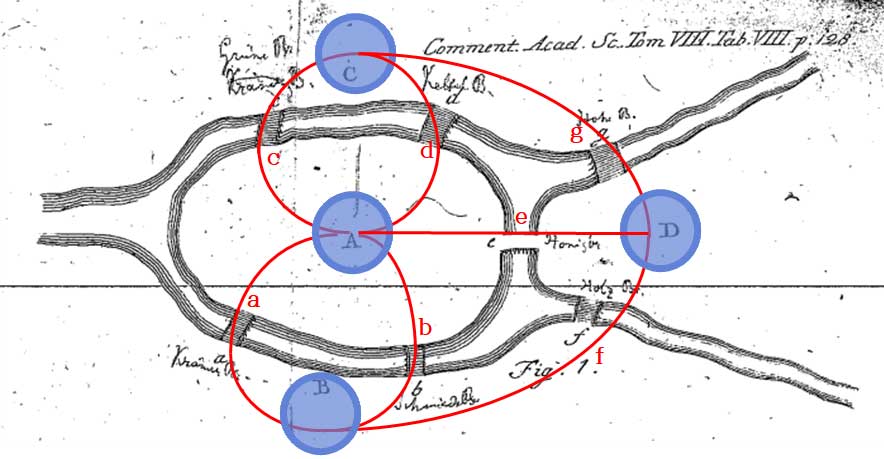
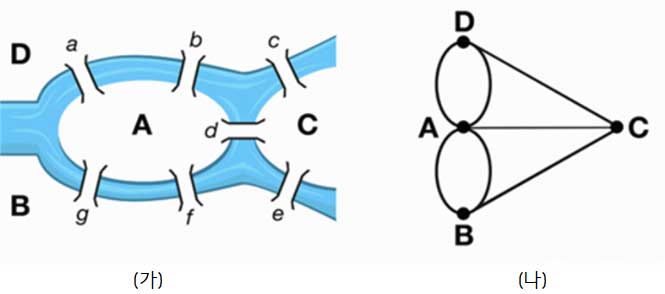
사실 아래의 그림 (가)도 쾨니히스베르크의 다리를 지도화한 것이기 때문에 그림 (나)는 지도의 지도, 즉 쾨니히스베르크의 다리를 메타지도화한 것이라고 말할 수 있다. 여기서 우리는 명백히 입구와 출구의 불일치를 확인할 수 있다. 오일러 경로는 도표의 방법론을 수학적으로 적용한 사례이다.
입구와 출구의 분열된, 고도로 자유로우면서도 고도로 조직된 도표를 만든 대표적인 수학자로는 데카르트(René Descartes)와 뉴턴(Isaac Newton) 그리고 라이프니츠(Gottfried Wilhelm Leibniz)가 있다. 이들 중에 획기적인 지도제작의 방법론을 창안한 이는 데카르트다. 그는 가로, 세로, 높이에 각각 x축, y축, z축이라는 단위 길이가 표시된 직선을 그음으로써 점, 선, 면을 수와 식으로 바꿔버렸다. 이제
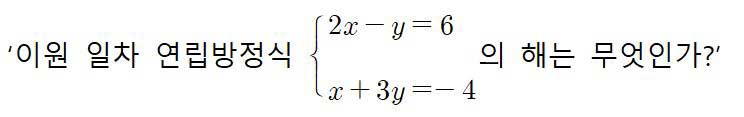
라는 대수학적 질문은 얼토당토않게도
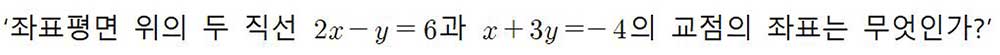
라는 기하학적 문제로 전환된다.
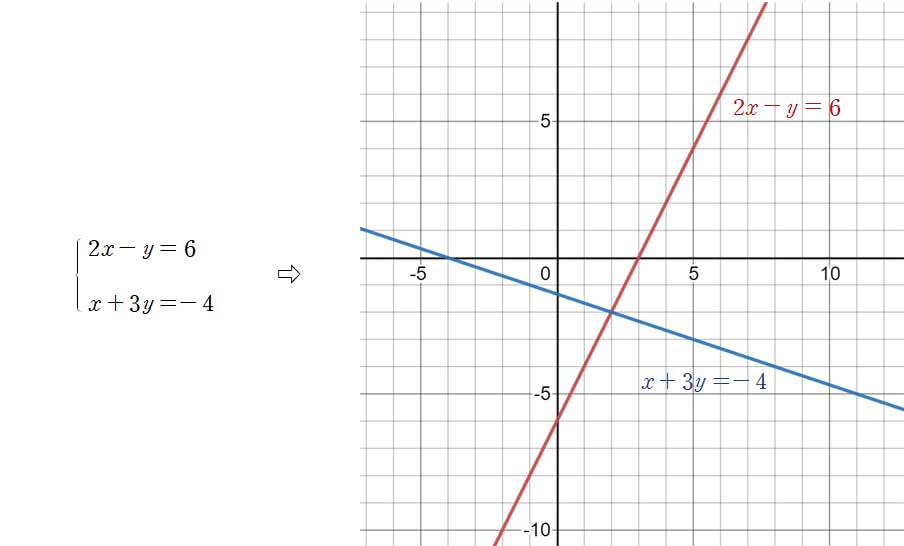
베이트슨(Gregory Bateson)이 적절하게 지적했듯이, 수학적 증명의 또 다른 전략은 ‘지도화(mapping)’나 엄격한 은유를 사용하는 것이다. 예를 들면, 대수학(algebraic) 명제는 기하학적 좌표 시스템으로 지도화될 수도 있으며, 기하학적 방법으로 증명될 수도 있다.3
이제 마지막으로 수학의 미적분과 도표의 관계에 대하여 생각해보자. 운동 법칙과 중력 법칙을 체계화한 뉴턴은 그 법칙들로부터 태양 주위를 도는 행성의 궤도에 관한 정확한 속성을 추정하는 작업에 착수했는데 그는 궤도의 형태를 한꺼번에 알아내려고 하는 몰적(molar) 접근 대신 궤도를 무한한 개수의 선분으로 나눈 뒤 태양의 중력이 각각의 무한소 선분에서 행성의 속도에 미치는 효과를 전부 더하는 분자적(molecular) 접근을 채택한다.
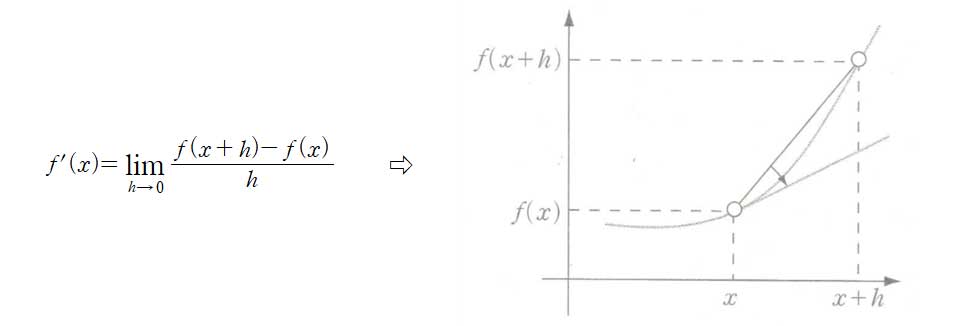
일반적으로 속력이란 스칼라량으로서 물체가 이동한 거리를 걸린 시간으로 나눈 값을 의미한다. 이에 반해 속도는 벡터량으로서 한 점에서의 순간 속도를 의미한다. 그것은 0에 가까울 정도로 작은 두 양의 비로 정의된다. [그림 5]에서 는 0에 접근하지만 절대로 0에 도달하지 않는 양을 의미한다. 따라서
일반적으로 속력이란 스칼라량으로서 물체가 이동한 거리를 걸린 시간으로 나눈 값을 의미한다. 이에 반해 속도는 벡터량으로서 한 점에서의 순간 속도를 의미한다. 그것은 0에 가까울 정도로 작은 두 양의 비로 정의된다. [그림 5]에서 는 0에 접근하지만 절대로 0에 도달하지 않는 양을 의미한다. 따라서
![]() 는 0에 접근하지만 절대로 0에 도달하지 않는 양을 의미한다. 따라서
는 0에 접근하지만 절대로 0에 도달하지 않는 양을 의미한다. 따라서 ![]() 는 대수학적 관점에서는 증분
는 대수학적 관점에서는 증분 ![]() 가 0에 가까워질 때 증가율
가 0에 가까워질 때 증가율 ![]() 의 극한을 의미하지만 기하학적 관점으로 볼 때 임의의 점
의 극한을 의미하지만 기하학적 관점으로 볼 때 임의의 점 ![]() 에서의 함수
에서의 함수 ![]() 의 접선의 기울기를 의미한다. 문제는 0에 접근하지만 절대로 0에 도달하지 않는다는 개념이 모호함을 넘어 위험하기까지 하다는 점이다. 뉴턴과 라이프니츠는 이 문제를 끝까지 해결하지 못했으나 코시(Augustin Cauchy), 바이어슈트라스(Karl Weierstrass), 데데킨트(Richard Dedekind) 등 후배 수학자들에 의해 결국 이 문제는 해결된다. 입구를 발견한 것이다.
의 접선의 기울기를 의미한다. 문제는 0에 접근하지만 절대로 0에 도달하지 않는다는 개념이 모호함을 넘어 위험하기까지 하다는 점이다. 뉴턴과 라이프니츠는 이 문제를 끝까지 해결하지 못했으나 코시(Augustin Cauchy), 바이어슈트라스(Karl Weierstrass), 데데킨트(Richard Dedekind) 등 후배 수학자들에 의해 결국 이 문제는 해결된다. 입구를 발견한 것이다.
미적분은 고도로 자유로우면서도 고도로 조직된 도표의 대표적 사례라고 할 수 있다. 입구를 발견하기 위해 지난한 과정을 거쳤지만 이를 통해 수많은 출구들이 발명된다. 이언 스튜어트는 “미적분을 적용할 수 있는 일들을 모두 나열하느니 차라리 이 세상에서 나사돌리개를 이용해서 할 수 있는 모든 일을 나열하는 편이 더 쉬울지도 모른다”고 말했다. 실제로 “세계를 바꾼 방정식”으로 불리는 푸리에 변환, 나비에-스토크스 방정식, 맥스웰 방정식, 슈뢰딩거 방정식, 블랙-숄스 방정식 등은 미적분 – 엄밀하게 말하면 미분 방정식 – 을 통해 기술된 자연의 모형들이다.4