‘[리토르넬로 시리즈] ①탈주선을 찾아서’에서는 음악에서 후렴구로 사용되는 리토르넬로의 예를 실제음악을 통하여 살펴보았습니다. 만약 반복되는 후렴구를 들으며 지루한 일상을 느꼈다면 우리는 일상의 탈주선을 찾아야할 것입니다.
이번 글에서는 『천개의 고원』 리토르넬로편에 나오는 리토르넬로라는 전반적인 개념을 이해함에 있어 구체적인 음악 안에서 어떻게 이해될 수 있는지, 사례를 통하여 알아보고자 합니다. 보통 어떤 글을 쓰는 사람이 그 주제에 대하여 모든 것을 다 이해하고 쓴다고 알고는 있지만, 다른 한편으로는 글의 주제를 보다 깊이있게 이해하기 위하여 쓰는 사람도 있다는 것을 저는 믿습니다. 제가 후자에 속한다는 것을 이해해 주시고, 함께 리토르넬로를 찾아 나섰으면 좋겠네요.
들뢰즈와 가타리는 『천개의 고원』 리토르넬로편에서 ‘카오스에서 환경과 리듬이 나온다’고 설명하였습니다. 그 말은 카오스 안에서 어떠한 성분의 주기적 반복으로 코드화가 이루어지고 그 주기적인 반복 속에서 차이가 발생, 리듬을 형성하며 그 리듬은 코드변환에 따라 다른 환경으로 이동한다고 합니다.
음악에 있어 코드와 리듬은 꽤 흔하고 중요한 용어들입니다. 실제 음악용어로서 많이 사용되는 용어이기도 하고요. 그런 것을 감안해보면, 들뢰즈와 가타리가 설명한 기본 전제인 리토르넬로의 기본 개념들은 집약된 표현 예술의 한부분인 음악에서 잘 들어맞으리라는 생각이 듭니다.
기보법에 대한 많은 논의가 있지만 우리의 이해를 돕기 위해 일반적으로 통용되는 기보법을 이용하겠습니다. 나머지 개념 또한 일반적인 음악적 용어들로 설명하겠습니다. 아직 음악에서 ‘빠르기’는 가변적이라 가정하겠습니다.
카오스라는 수많은 성분 중에 하나의 음이 있었습니다. 이 음을 ‘도’라고 가정하시죠.

사실 이 음도 수없이 많은 진동 속에서 262Hz로 진동하는 소리라고 합니다. 물론 이 음도 카오스 중에 무수한 음들 중 하나겠지요. 아무튼, 사람들은 이 음을 ‘도’라고 칭하였고 이 ‘도’와 어울리는 음들을 찾게 되지요. 정확히는 진동을 함께 하였을 떄 잘 맞는(?) 음들이 함께 하게 됩니다.
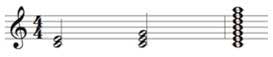
음악에서는 세 가지 음이 함께 할 때 코드라고 이름 짓습니다. 위의 예에서 첫 번째 마디 두 번째 세 개의 음들을 실용음악에선 C 코드라고 부릅니다. 물론 클래식에서는 이것을 I 라고도 하고 다른 음악 쟝르에서는 다르게 표기할 수도 있겠습니다. 어쨌든 세음이 쌓였을 때 코드라 명명합니다. 음악에서 말하는 코드와 리토르넬로에서 말하는 코드화는 정확히 일치하지 않는 개념일 수도 있습니다만 코드화라는 것을 음악적인 좁은 의미인 ‘코드’로 설명해봅니다. 그리고 7개음 – 도레미파솔라시, 영어로 CDEFGAB라고 하겠습니다 – 이 쌓여져 있는 ‘환경’ 이 만들어지죠. 이 환경은 서로의 주파수들끼리 잘 맞는 음들이라는 것입니다. ‘잘 맞’다는 것은 인간의 귀로 들을때 잘 어울리는 음들을 찾아 정리한 것이라고 생각해도 되겠습니다.
자, 이제 환경이 만들어졌습니다. 우리가 학교에서 배웠던 다장조군요. 영어로하면 C major Key입니다. 곧, C Key – C가 도라는 뜻입니다. 만약 ‘미’인 E가 ‘도’면 E Key가 됩니다 – 라는 환경이 만들어졌습니다. 앞에서 언급하였듯이, 이 속에서 더욱 잘 맞는 음들의 배합이 일어나는데요. 이것이 바로 코드화입니다. C 코드뿐만이 아닌 Dm, Em, F, G, Am, Bmb5 – ‘m’은 마이너 (단조)를 뜻하고 m이 없는 코드는 메이저 (장조)를 뜻합니다.

자, 이제 리듬을 만들어 볼 시간입니다. 우선 여기서 박자 개념이 나옵니다. 이 예에서는 4/4박자를 가지고 있습니다. 이는 4분음표인 Œ가 한마디에 4개가 있다는 뜻입니다. 4/4박자라고 단정됨에 따라 이는 불변한 것이 됩니다. 아무리 음들과 리듬, 빠르기가 발버둥쳐 봤자 4/4박자 안에서 밖에 놀 수 없습니다. 마치 우리의 짜여진 일상과 같이 말입니다.
하지만 리듬은 어떨까요? ‘항상 코드변환을 담고 공동의 척도를 가지지 않는 것으로 비판적입니다’ 라고 들뢰즈와 가타리가 설명합니다. 과연 그럴지 한번 볼까요?
우선, 정해진 박자 안에서 같은 환경 안에서 코드들이 모여 소리를 내기 시작합니다.

리듬을 형성시켜 보겠습니다.

위의 첫 번째 예에서는 C코드로 시작하여 C 코드로 끝났습니다. 같은 환경 안에서 시작하여 같은 환경 안에서 끝맺음을 했네요. 하지만 두 번째 예에서는 끝부분이 다소 의아한 분위기를 자아냅니다. 보셨듯이 Eb으로 끝맺음을 합니다. 곧, Eb Key 라는 다른 환경으로 이동하였습니다. 네 번째 마디에서 종래 F, G코드가 Eb Key에서 가능한 ‘음’들인 Ab, Bb조각들을 자신의 코드내로 받아들인 것이죠. 그래서 Eb Key에서 자연스러운 코드진행인 Fm, Bb → Eb 로 진행하며, 다른 환경인 Eb Key, 다른 조의 환경판이 열렸습니다. 한편, 종래의 C Key환경에서 보자면 F코드가 Fm로 바뀌면서 무언가 긴장감을 주었습니다. 전 이 긴장감을 리듬이라 생각하여 소개하고 있는 것입니다. 결론적으로, 위 예의 4번째 마디의 Fm, Bb 코드는 C Key 와 Eb Key 둘-사이의 리듬을 형성하였습니다.
차원이 다를 뿐 하나의 음이 다른 음들을 만나 코드 – C, Em, Am, F, G 코드 등 – 를 이루는 것 또한 리듬발생으로 볼 수도 있겠고, 하나의 코드가 다른 코드로 이행 – C → Em, Em → Am… 되는 것도 좁은 의미의 리듬의 발생이라고도 할 수 있겠습니다. 단지 차원이 다른 문제라고 생각됩니다. 이 예에서 중요한 것은 C Key에서 없었고 Eb Key에서 존재하는 – 존재할 가능성이 더 많은 Ab, Bb 음들을 받아들임으로써 리듬을 형성, 새로운 판인 Eb Key로 환경이 변화하였다는 것입니다. 사실 이러한 조바뀜 (modulation) 예는 흔한 예입니다. 특히나 클래식이나 재즈에선 말이죠.
위에서 제가 든 예에 멜로디가 없다는 점이 다소 부자연스럽습니다. 만약 우리가 멜로디를 넣는다면, 그때야 비로소 환경과 리듬의 영토화가 시작되는 것이라 생각합니다. 환경과 리듬이 영토화하는 것이 “지표들”에 의하여 진행된다면, 그 “지표들”이 바로 수평적 – 지금까지는 수직적인 음들이었다면 – 인 멜로디라는 것이죠. 실제로 어떤 코드 진행이 하나의 음악을 표현하기도 하지만 멜로디와 함께 하면서 그 표현의 강도는 강해지는 것이 사실입니다. 여기에서 또 다른 리듬을 만날 수 있는 것 같습니다. 표현성을 가지는 리듬의 행위, 그리고 질을 획득해 나가는 환경성분의 행위가 그것입니다.
들뢰즈와 가타리는 이를 리듬 또는 ‘선율의 표현-되기’ 그리고 ‘고유한 질’이라 칭하였습니다.
서명, 부호, 포스터, 플래카드 등으로 일컫는 멜로디를 한번 구성해보려 합니다. 그리고 그 멜로디가 영토성을 가지는 모티프와 대위법으로 발전되는 것을 구체적인 음악의 예로 찾아보려 합니다. 다음번에 말이죠.


